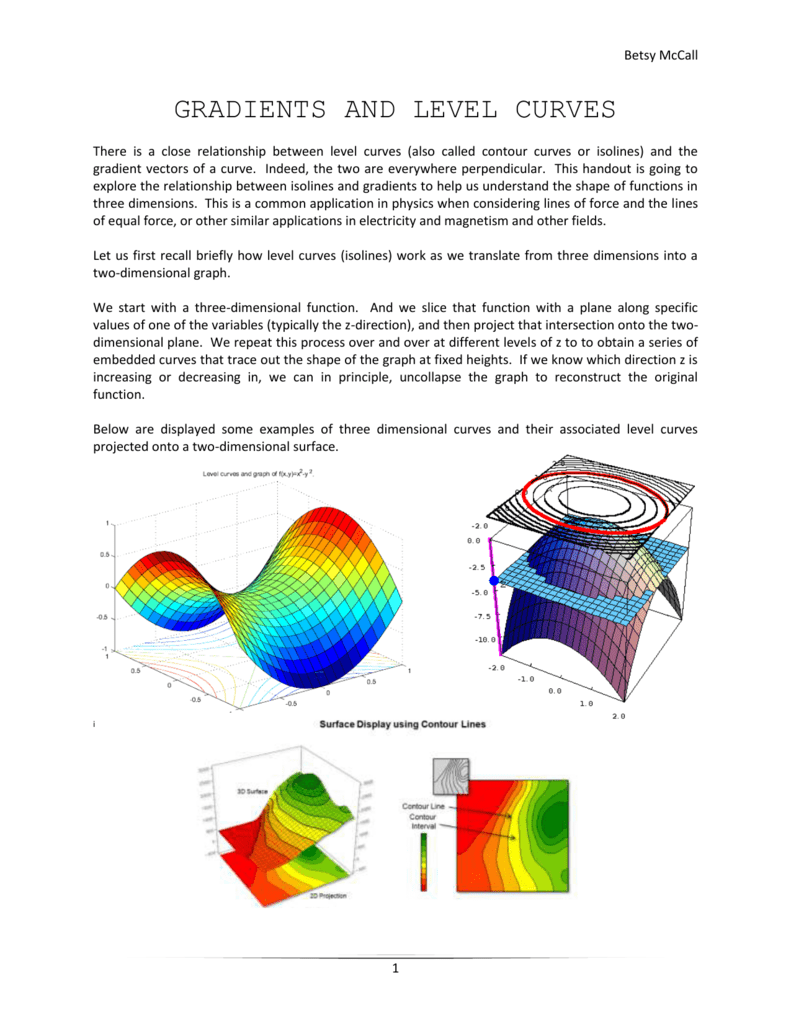
Level Curves and Level Surfaces Line Integrals Optimization and Related Rates Optimization for Functions of 2 Variables Parametric Equations 2space Parametric Equations 3space Partial Derivatives Polar Coordinate System Polar Coordinates Derivatives and Integrals PreCalculus Riemann Sums and the Fundamental Theorem of Calculus 2dPractice problems Sketch the level curves of Sketch the threedimensional surface and level curves of Consider the surface At , find a 3d tangent vector that points in the direction of steepest ascent Find a normal vector to the surface at the point Give the equation for the tangent plane to the surface at the point The bellshaped curve is a common feature of nature and psychology The normal distribution is the most important probability distribution in statistics because many continuous data in nature and psychology displays this bellshaped curve when compiled and graphed For example, if we randomly sampled 100 individuals we would expect to see a

3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com
Level curve examples
Level curve examples-Level Curves So far we have two methods for visualizing functions arrow diagrams and graphs A third method, borrowed from mapmakers, is a contour map on which points of constant elevation are joined to form contour curves, or level curves A level curve f (x, y) = k is the set of all points in the domain of f at which f takes on a given value kHigher indifference curves represent a greater level of utility than lower ones In Figure 1, indifference curve Ul can be thought of as a "low" level of utility, while Um is a "medium" level of utility and Uh is a "high" level of utility All of the choices on indifference curve Uh are preferred to all of the choices on




Plotting Using Contour In Python Epythonguru
1 In your first example, the proper solution is y = ± k − x 2 You left out the plusorminus That is not a small thing there are usually two values of y for each x, and that greatly affects the plotting of the curves I would say that there is no single general method for finding level curves, in a similar way that there is no generalExample 7 Describe the level curves of the function f(x,y) = x2 y2 from Examples 2 and 3 Answer Figure a shows horizontal cross sections of the graph of f and Figure b shows the corresponding level curves • The level curve f = c is the circle of radius √ c with its center at the origin if c > 0, is the origin if x = 0, and is empty Curves may be extremely powerful, going far beyond what can be accomplished with Levels, but once you understand how it works, Curves is actually very simple In fact, it's as simple as, well, drawing curves!
The level curves are just the horizontal traces of the graph of f Example The function z = f(x,y) = x3 − y has as its domain D the whole xyplane and as its range the whole real line The level curves of f are the curves x3 −y = k lying in the xyplane for any value of k These level curves are the graphs of the cubic function y = x3 −Level Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c Indifference Curve An indifference curve represents a series of combinations between two different economic goods, between which an individual would be theoretically indifferent regardless of
Example, the set Sis in R2 This gure also illustrates the fact that a ball in R2 is just a disk and its boundary18 23 An example of in nitely many alternative optimal solutions in a linear programming problem The level curves for z(x 1;x 2) = 18x 1 6x 2 are parallel to one face of the polygon boundary of the feasible region MoreoverLevel curves allow to visualize functions of two variables f(x,y) Example For f(x,y) = x2 − y2 the set x2 − y2 = 0 is the union of the lines x = y and x = −y The set x2 − y2 = 1 consists of two hyperbola with with their "noses" at the point (−1,0) and (1,0) The set x2 − y2 = −1 consists of two hyperbola with their noses at (0,1) and (0,−1) Drawing several contour curves {f(x,y) = c }Examples f(x,y)=cos(y)esinx f(x,y)=4−x2 −y2 2 44 2 x y 2 42 0 2 1 22 1 r t 1 2 0 1 2 3 4 Mth 254H – Winter 13 3/7 Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations



The Gradient And Directional Derivative




Level Curves Examples Level Surface
Answered 3 years ago A level curve can be drawn for function of two variable ,for function of three variable we have level surface A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve ofWe discuss level curves what are they, how do you find them, and what do they look like? Now on to the real problem The level curves (or contour curves) for this surface are given by the equation are found by substituting \(z = k\) In the case of our example this is, \k = \sqrt {{x^2} {y^2}} \hspace{025in}\hspace{025in} \Rightarrow \hspace{025in}\hspace{025in}{x^2} {y^2} = {k^2}\ where \(k\) is any number



Examples Wednesday Feb 19




Calculus Iii Functions Of Several Variables
We have done this in Example 4 at level curves Unfortunately, sometimes it is not possible to rewrite the level curve Unfortunately, sometimes it is not possible to rewrite the level curve However, even in that case we can determine the slope of the tangent line to the level curve by the use of the following ruleIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the functionLevel Curves and Surfaces The graph of a function of two variables is a surface in space Pieces of graphs can be plotted with Maple using the command plot3dFor example, to plot the portion of the graph of the function f(x,y)=x 2 y 2 corresponding to x between 2 and 2 and y between 2 and 2, type > with (plots);



2



8 Calculus Of Several Variables Functions Of Several Variables Ppt Download
Another example is the two variable realvalued function $f(x, y) = x^2 y^2$ which represents a hyperboloid The level curves generated by the planes $z = 1$, $z = 2$, and $z = 3$ are hyperbolas The image below depicts the level curve of this hyperboloid corresponding to $z = 1$Try to visualize these level curves lifted up to form a surface and compare; How to Use the Learning Curve Theory (with Examples) The learning curve theory is a way to understand the improved performance of an employee or investment over time The idea is that the more an employee does something, the better they will get at it, which translates to lower cost and higher output in the long term




Functions Of Several Variables
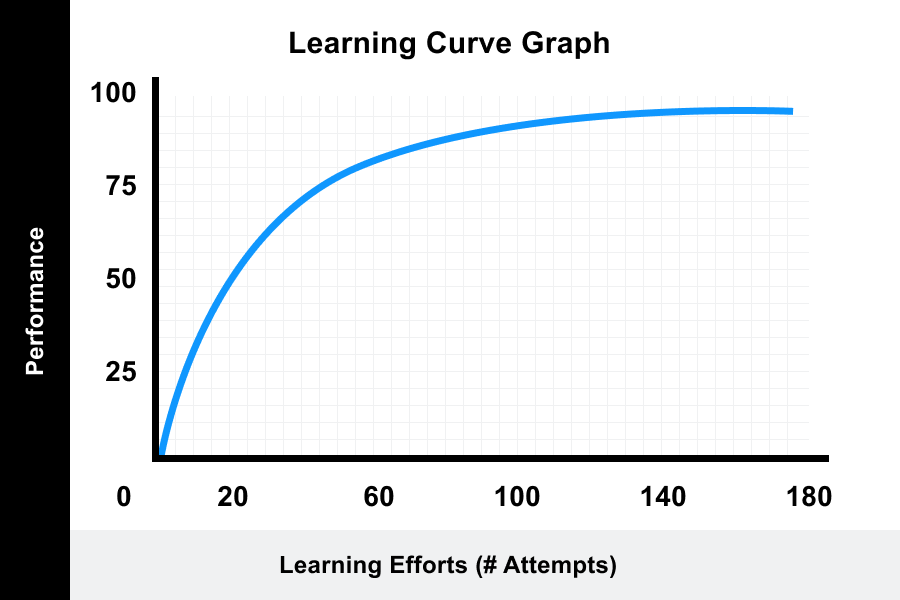



Learning Curve Theory Meaning Formulas Graphs
Perpendicular to the Level Curve TheoremThe gradient isalways perpendicular to the level curve through its tail Proof We will only show this for a surfa ce z f(x,y) whose level curve c f(x,y) can be parameterized by(x(t),y(t)) Then atangent vector on the level curve can be described by (x'(t),y'(t)) ff Next, the gradient is f(x,y) , xy Level sets show up in many applications, often under different names For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an implicit equation Analogously, a level surface is sometimes called an implicit surface or an isosurfaceThe level curve of this function for the value 2 is empty (there are no values of (x, y) such that f(x, y) = 2) and the level curve for the value 1 is the set all all points (x, y) In less extreme examples, some but not all level curves are sets Consider a basically conical mountain, with terraces at heights of and 40;



Pdf A Fast Iterative Method For Eikonal Equations Semantic Scholar




Matb41h3 Midterm Detailed Examples For Drawing Level Curves Oneclass
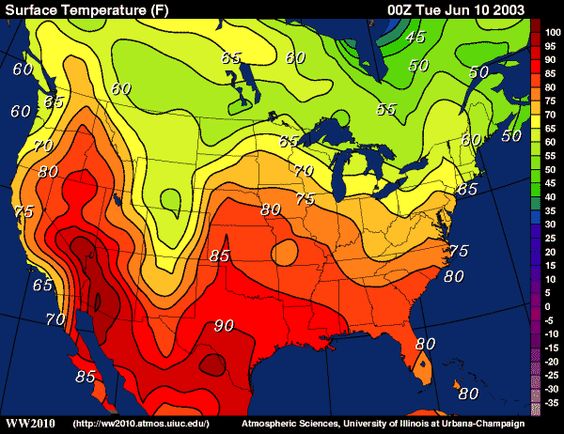
U(x;y) = cas the curve which represents the easiest walking path, that is, altitude does not change along that route The altitude is conserved along the route, hence the terminology conservation law Other examples of level curves are isobars and isotherms An isobar is a planar curve where the atmospheric pressure is constant An isotherm is a planar curve along which the temperature is Its graph is shown below From the side view, it appears that the minimum value of this function is around 500 Example 4 f (x,y)=2e (x1)2y2 3e (x2)2 (y1)2 2e (x1)2 (y2)2 A level curve of a function f (x,y) is a set of points (x,y) in the plane such that f (x,y)=c for a fixed value c Example 5It looks much like a topographic map of the surface




Functions Of Several Variables



2
For example, "tallest building" Search for wildcards or unknown words Put a * in your word or phrase where you want to leave a placeholder For example, "largest * in the world" Search within a range of numbers Put between two numbers For example, camera $50$100 Combine searches Put "OR" between each search query For example, marathon Sketch several traces or level curves of a function of two variables The function might map a point in the plane to a third quantity (for example, pressure) at a given time The method for finding the domain of a function of more than two variables is analogous to the method for functions of one or two variablesThe level curves f(x,y) = k are just the traces of the graph of f in the horizontal plane z=k projected down to the xyplane Figure 1 Relation between level curves and a surface k is variating acording to 5015 One common example of level curves occurs in topographic maps of mountainous regions, such as the map in Figure 2 The level curves are curves of constant elevation of the




Level Curves Calculus




Calculus Iii Functions Of Several Variables
This Service Has Been Retired Faculty profile information has been migrated to UMassD Sites and the University's DirectoryShare a link to this widget More Embed this widget » Added by RicardoHdez in Mathematics The level curves of f (x,y) are curves in the xyplane along which f has a constant value Send feedback Visit WolframAlpha5 Plot the level curves by adding a 2D Graph page to the document and plotting the lists as f1(x)and f2(x) Modify the colors of the level curves if desired The examples use the color green for positive values of z, blue for z = 0, and orange for negative values of z 6 Use the Settings Settings dialog to hide the plot labels 7



Level Curves And Contour Plots Mathonline




Level Curves Of Functions Of Two Variables Youtube
In this first look at Curves, we'll compare it with the Levels command to see just how similar the two really areWe can plot the level curves for a bunch of different constants c together in a level curve plot, which is sometimes called a contour plot We return to the above example function f ( x, y) = − x 2 − 2 y 2 For some constant c, the level curve f ( x, y) = c is the graph of c = − x 2 − 2 y 2For example the curve at height z = 1 is the circle x2 y2 = 1 On the graph we have to draw this at the correct height Another way to show this is to draw the curves in the xyplane and label them with their zvalue We call these curves level curves and the entire plot is called a contour plot For this example they are shown in the plot on




Level Curves In Mathbb R 3 Mathematics Stack Exchange



Level Curves And Contour Plots Mathonline
The level curves are shown in Figure 124(a) Note how the level curves for \(c=0\) and \(c=02\) are very, very close together this indicates that \(f\) is growing rapidly along those curves Figure \(\PageIndex{4}\) Graphing the level curves in Example 1214 In Figure \(\PageIndex{4b}\), the curves are drawn on a graph of \(f\) in spaceLevel Curves and Surfaces Example 2 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level setAs in this example, the points $(x,y)$ such that $f(x,y)=k$ usually form a curve, called a level curve of the function A graph of some level curves can give a good idea of the shape of the surface;




Level Curves




Functions Of Several Variables
LEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;A level curve of a function is curve of points where function have constant values,level curve is simply a cross section of graph of function when equated to some constant values ,example a function of two variables say x and y ,then level curve is the curve of points (x,y) ,where function have constant value Can be better understood by an example Find the level curves of heightsLevel Curves and Surfaces Example 3 In mathematics, a level set of a function f is a set of points whose images under f form a level surface, ie a surface such that every tangent plane to the surface at a point of the set is parallel to the level set




Calculus Iii Functions Of Several Variables




Level Set Wikipedia
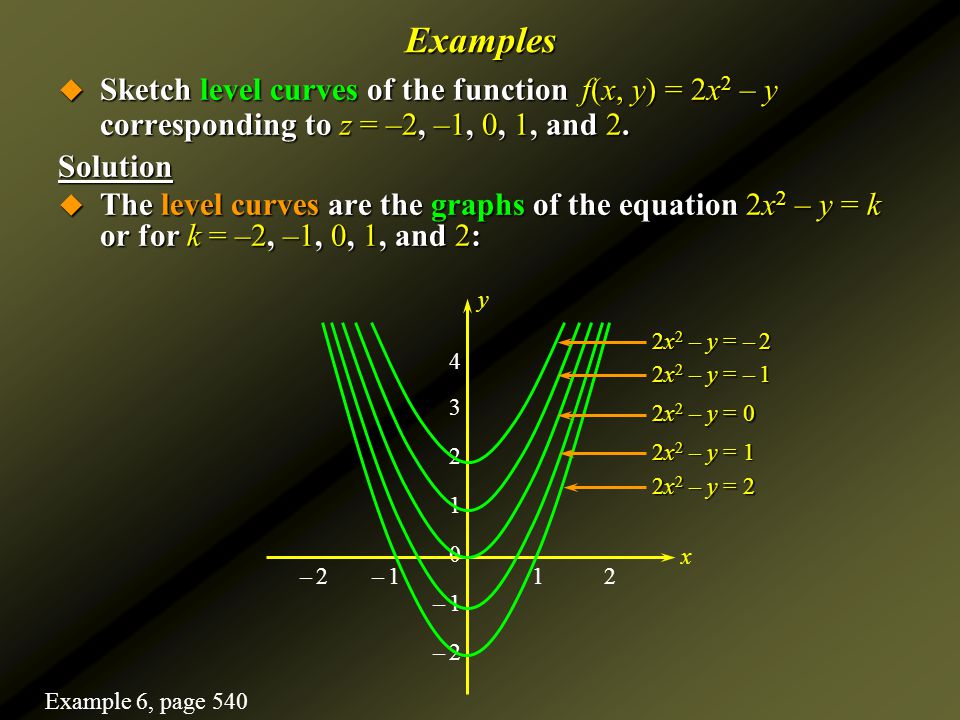
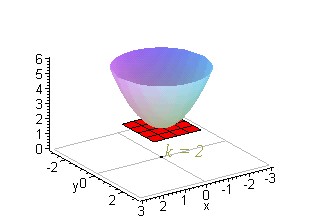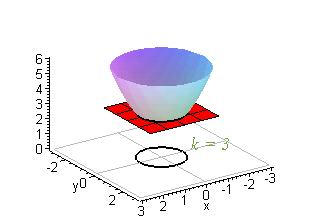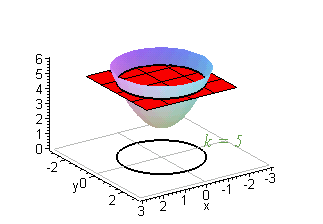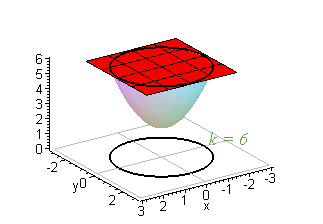
Question EXAMPLE 11 Sketch the level curves of the function g(x, y) = √64 x² y2 for k=0, 6, 7, 8 SOLUTION The level curves are √64 x² y2 = x or x y² = 64 – K² This is a family of concentric circles with center (0,0) and radius 8k The cases k = 0, 6, 7




Multivariable Functions And Level Curvesi M Having A Chegg Com




Visualizing Surface And Level Curves Youtube



Http Userweb Eng Gla Ac Uk Trevor Davies Maths2 T1 Pdf



Level Set Examples Math Insight



Level Curves




A Full Guide On Leveling Different Curves Tips And Examples Enjoy Bobstavern




Level Curves




Level Set Wikipedia




Level Curves Examples Done In Mathematica Last Modified Spring 14




How Can I Project Level Curves Onto The Axis Planes In 3d General Usage Julialang




How To Sketch Level Curves Youtube



1




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




3 Points Writing Prompt 1 Typed 100 0 Words In Chegg Com



Reading Aggregate Demand Macroeconomics



1



Gradients And Level Curves




Plotting Using Contour In Python Epythonguru




Level Set Examples Math Insight
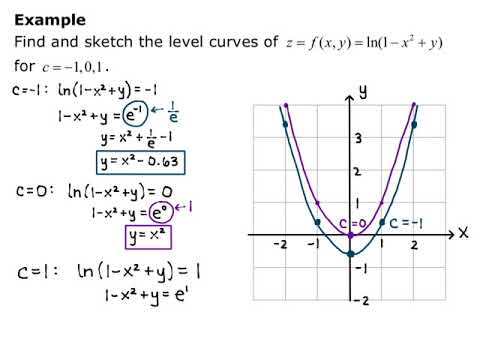



Section 13 1 Level Curves Youtube




Subimages And Level Curves For The Image Examples In Fig 8 Download Scientific Diagram



Relief Functions And Level Curves




Level Curves Examples




Level Curves Examples Done In Mathematica Last Modified Spring 14




Level Set Wikipedia




Graphs And Level Curves



2




Matlab How Can I Get The Expression Of The Level Curves Of A Function Stack Overflow




How To Read A Sea Level Curve Geological Digressions




Examples Of Level Curves For Different Types Of Functions Calculus Coaches




Level Curves Examples Done In Mathematica Last Modified Spring 14




Examples Of Two Relative Sea Level Curves From The Disko Bugt Area The Download Scientific Diagram



Diurnal Cortisol Curves




Some Examples Of Graphs Used In The Problems A Level Curves Of A Download Scientific Diagram




Ppt Functions Of Several Variables Partial Derivatives Powerpoint Presentation Id




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube




Level Curves Examples Level Surface




How To Sketch Graphs For Functions Of Two Variables Chris Tisdell Unsw Youtube




Level Sets Ximera



Calculus Iii Functions Of Several Variables




Two Examples Of Eustatic Sea Level Curves That Show Significant Download Scientific Diagram



Level Curves And Contour Plots



1



Level Curves And Contour Plots Mathonline




Level Curves Examples Level Surface




Example 11 Sketch The Level Curves Of The Function Chegg Com



Gradients Level Curves



S0 3




3 Points Writing Prompt Typed 100 0 Words In Chegg Com



Functions Of Several Variables Ximera



S0 3




Level Curves Examples Level Surface
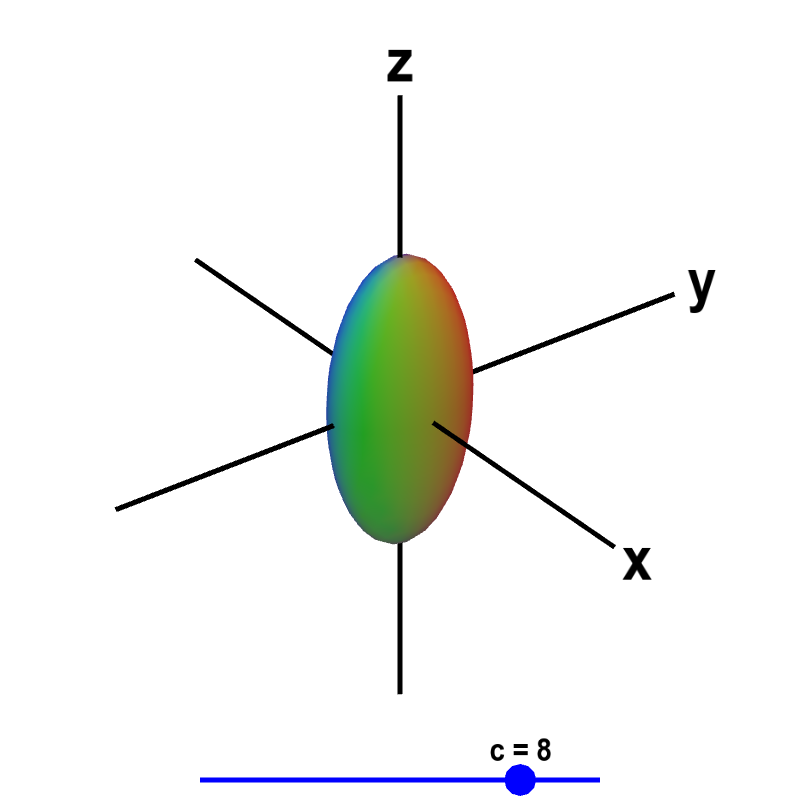



Level Sets Math Insight
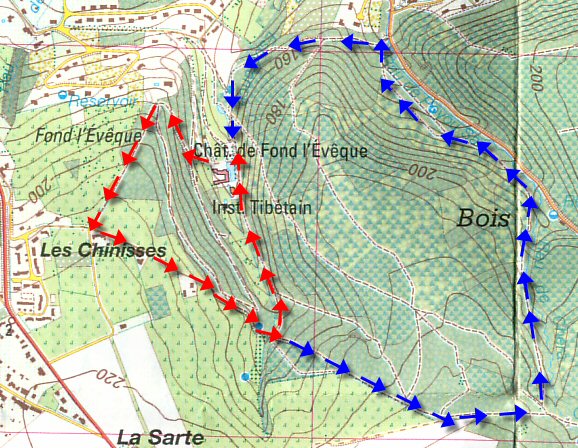



Extra Explanation Wiskunde Op Tilburg University




Level Set Wikipedia




Level Sets Math Insight
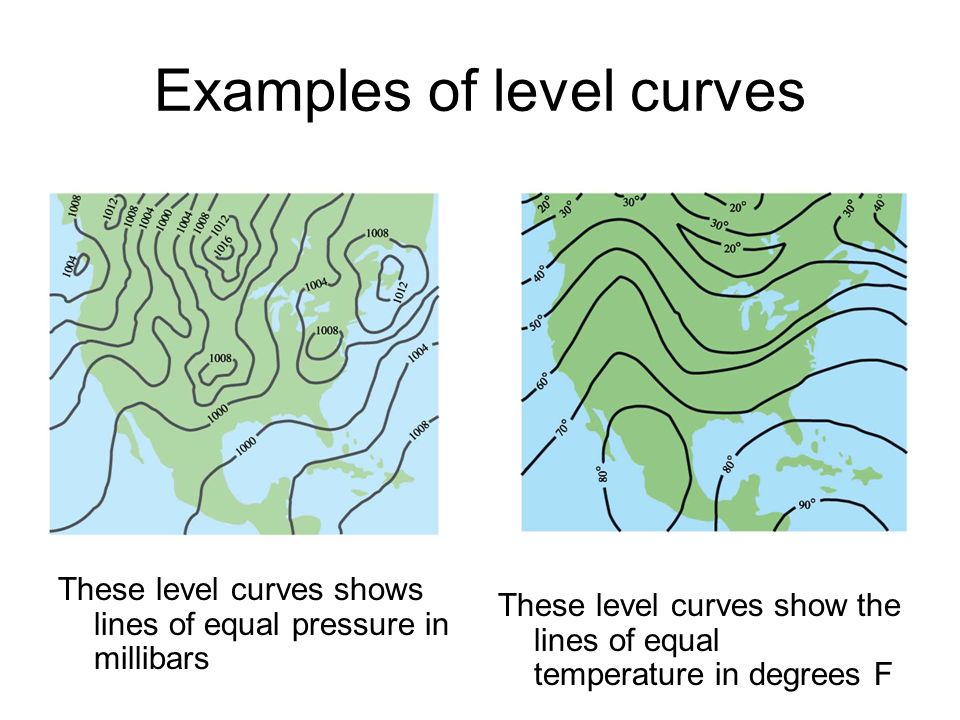



13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned




Applicable Mathematics 2 Examples 1 Level Curves



Solved Define The Level Curves Of A Function Of Two Variables Give Examples Of Several Surfaces Whose Level Curves Are Circles And At Least One Ex Course Hero



Http Math Oregonstate Edu Garity 254h Winter13 Notes 10 Graphs Levelcurves Pdf




Applicable Mathematics 2 Examples 1 Level Curves



S0 3



Math 225 Calculus Iii




In Calculus I And Ii We Worked With Functions Chegg Com



Math 225 Calculus Iii



1




Level Sets Math Insight



Http Www Ams Sunysb Edu Jiao Teaching Ams261 Fall12 Lectures Larcalc9 Ch13 Pdf



Equal Loudness Curves
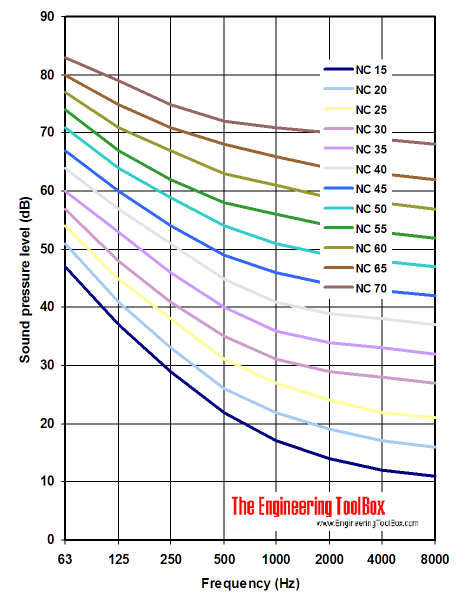



Nc Noise Criterion



Level Sets Ximera




Level Curves
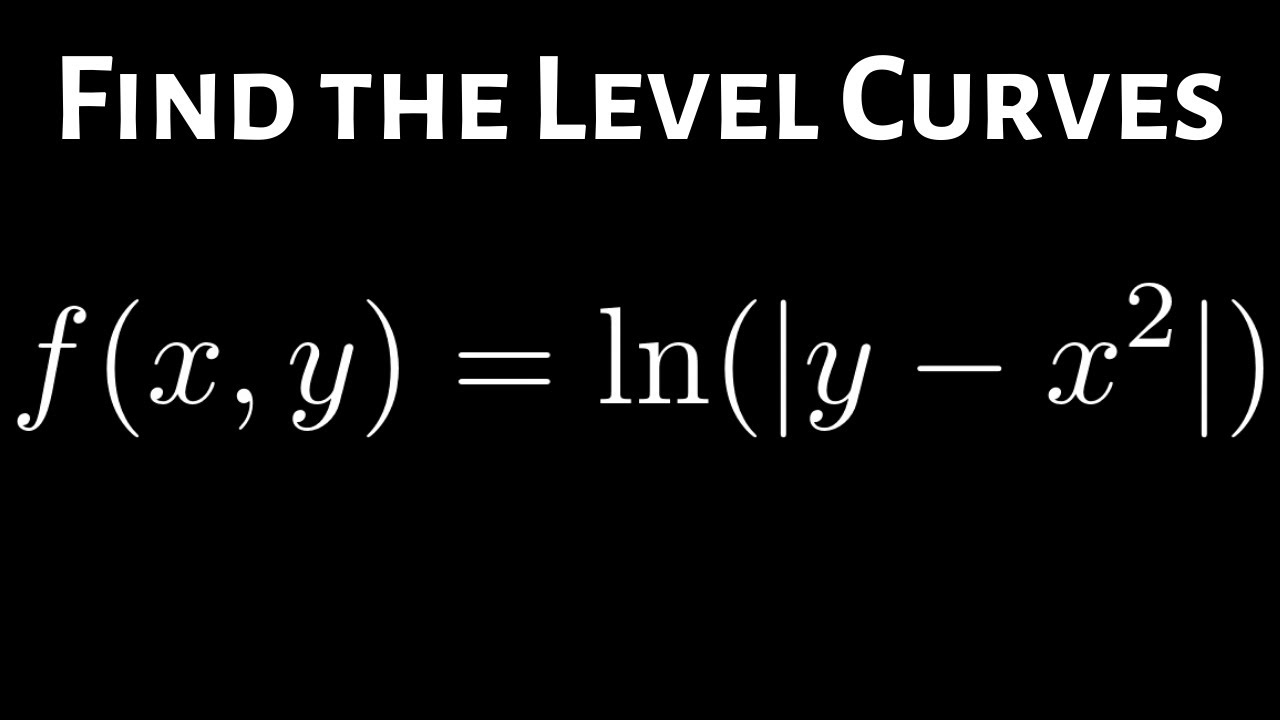



How To Find The Level Curves Of F X Y Ln Y X 2 Youtube




Level Set Examples Math Insight




2
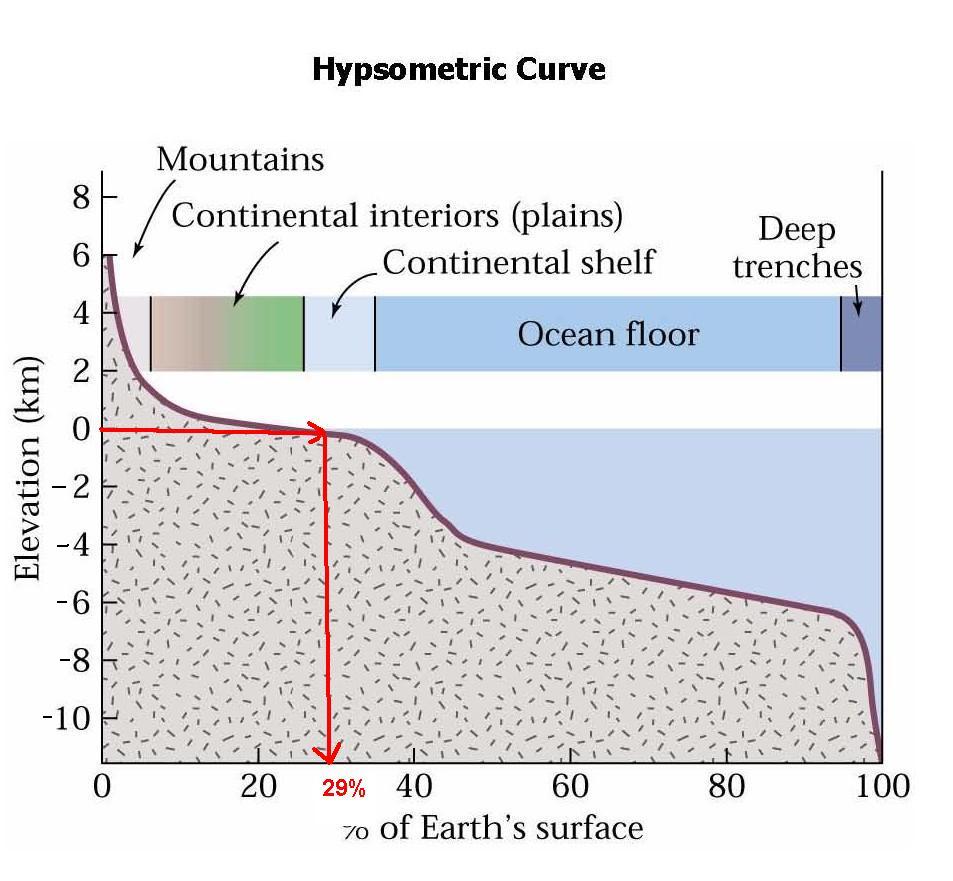



Hypsometric Curve




Fun Math Art Pictures Benice Equation Scilab Example Plotting Implicit Curves Level Curves
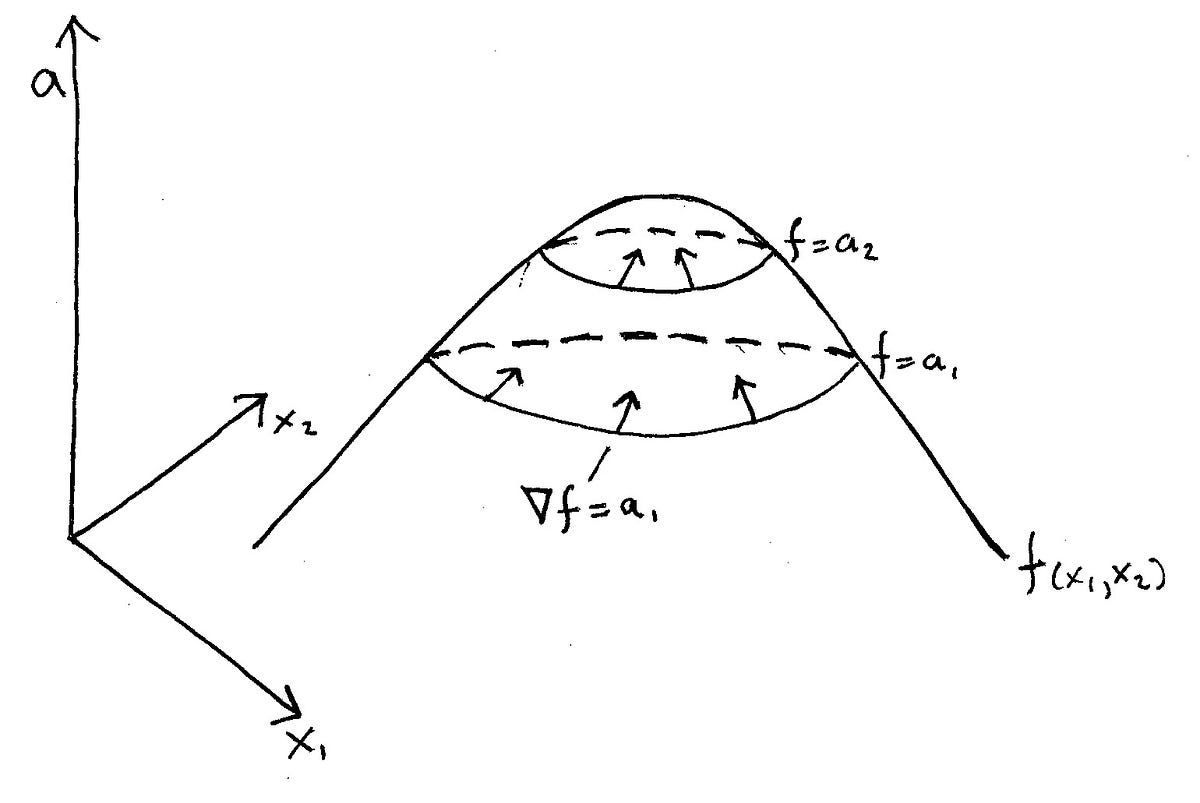



A Simple Explanation Of Why Lagrange Multipliers Works By Andrew Chamberlain Ph D Medium




Calculus Iii Functions Of Several Variables




Level Sets Math Insight



Http Math Ucsd Edu Ashenk Math c Summer 10 Rog Sec 14 1 P 1 Pdf




Graphs And Level Curves



0 件のコメント:
コメントを投稿